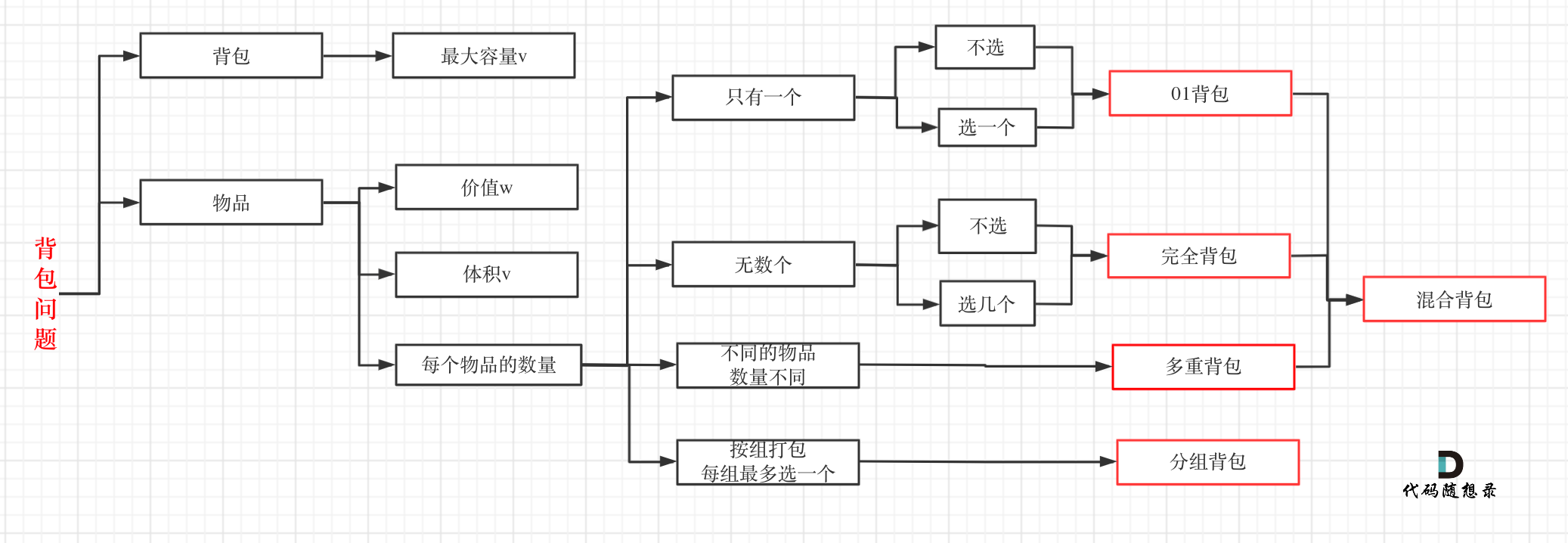
背包问题

01 背包

01 背包是基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。 用子问题定义状态：

即 表示前 件物品恰放入一个容量为 的背包可以获得的最大价值

状态转移方程：

可以通过倒着遍历进行转移，将第一维省去

复杂度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 5;

int f[N];

int main()
{
    int n, V;
    cin >> n >> V;
    for (int i = 1; i <= n; i ++ )
    {
        int v, w;
        cin >> v >> w;
        for (int j = V; j >= v; j -- )
        {
            f[j] = max(f[j], f[j - v] + w);
        }
    }
    cout << f[V] << endl;
    return 0;
}

装箱问题

给定 个物品，每个物品有一体积 ，有一个总体积为 的箱子，求剩余体积最小为多少？

用 表示体积不超过 的情况下的最大体积，则剩余体积为 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 5;

int f[N]; // f[i]表示体积不超过i的组合中最大能达到多少

int main()
{
    int V, n;
    cin >> V >> n;
    for (int i = 1; i <= n; i ++ )
    {
        int v;
        cin >> v;
        for (int j = V; j >= v; j -- )
        {
            f[j] = max(f[j], f[j - v] + v);
        }
    }
    cout << V - f[V] << endl;
    return 0;
}

二维费用的背包问题

01 背包的动态转移方程是

那么这个多了个重量，那么可以再开一维，变成三维

同 01 背包，它也可以压缩亿下空间，于是变成了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 105;

int f[N][N];

int main()
{
    int n, V, M;
    cin >> n >> V >> M;
    for (int i = 1; i <= n; i ++ )
    {
        int v, m, w;
        cin >> v >> m >> w;
        for (int j = V; j >= v; j -- )
        {
            for (int k = M; k >= m; k -- )
            {
                f[j][k] = max(f[j][k], f[j - v][k - m] + w);
            }
        }
    }
    cout << f[V][M] << endl;
    return 0;
}

宠物小精灵之收服

花费 1：精灵球数量 花费 2：皮卡丘体力值

相当于同时处理两个 01 背包

价值：小精灵的数量

状态表示： 表示所有只从前个物品中选，且花费 1 不差过 ,花费 2 不超过 的选法的最大价值

状态计算： 最多收服的小精灵数量 最大体力为 (要求剩余体力大于 1)

最少耗费体力怎么计算呢？找到最小的一个 k 满足 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1005;

int f[N][N]; // f[i][j]表示精灵球用了i个，皮卡丘体力用了j后能够收服的最多的精灵

int main()
{
    int n, M, K;
    cin >> M >> K >> n;
    for (int i = 1; i <= n; i ++ )
    {
        int m, k;
        cin >> m >> k;
        for (int j = M; j >= m; j -- )
        {
            for (int t = K - 1; t >= k; t -- )
            {
                f[j][t] = max(f[j][t], f[j - m][t - k] + 1);
            }
        }
    }
    cout << f[M][K - 1] << " "; // 用的体力不能超过K - 1，因为剩余的体力要大于1
    int k = K - 1;
    while(k > 0 && f[M][k - 1] == f[M][K - 1]) k -- ;
    // 倒着找回去，找一下能够使得捕获精灵球最多的情况下，最小花费的体力
    cout << K - k << endl;  // 求得是剩余的体力
}

潜水员

设所需氧气为 ，所需氮气为

题目的意思选择若干个气缸，可以使得 , 且重量尽量的轻。

即我们选择的气缸的氧气加起来至少为 ，氮气加起来至少为 。

在 01 背包的时候， 和 不能作为取值，因为我们背包的容量只有 和 ，放不下 和

但是在这里，假设我们把 和 装进背包，并不会有什么问题，因为 氧气和氮气 超出背包容量依然能

满足。如果不装来反而会漏更新状态， 所以可以通过一个取 max 的操作包含这一状态

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 22, M = 80;

int f[N][M];  // f[i][j] 表示费用1z至少是i, 费用2至少是j时, 重量的最低值

// 集合表示中为恰好是当前值时, 0赋值为0, 其他赋值为正无穷(求最小值)

int main()
{
    int n, m, K;
    cin >> n >> m >> K;
    memset(f, 0x3f, sizeof f);
    f[0][0] = 0;

    for (int i = 1; i <= K; i ++ )
    {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        for (int j = n; j >= 0; j -- )
        {
            for (int k = m; k >= 0; k -- )
            {
                f[j][k] = min(f[j][k], f[max(0, j - v1)][max(0, k - v2)] + w);
                //  关键的一个取max然后转移的过程
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

数字组合

可以转化为 01 背包问题求方案数：

将总和 看作背包容量；

将每个数的值 看作体积；

复杂度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

// 将M看成背包容量，将每个数看成一个物品，值看成体积
// 目标：求出总体积恰好是M的方案数

const int N = 105, M = 100005;

int f[M];
//  f[j]表示体积恰好是j的方案的集合

int main()
{
    int n, m;
    cin >> n >> m;
    f[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        int v;
        cin >> v;
        for (int j = m; j >= v; j -- )
            f[j] = f[j] + f[j - v];
    }
    cout << f[m] << endl;
    return 0;
}

完全背包

模板

与 01 背包类比

推导状态转移方程

故可以进行一个替换得到

此时可以将复杂度优化掉一层

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1005;

int f[N];
// f[j], 总体积不超过j的最大价值


int main()
{
    int n, V;
    cin >> n >> V;
    for (int i = 1; i <= n; i ++ )
    {
        int v, w;
        cin >> v >> w;
        for (int j = 0; j <= V; j ++ )
        {
            if(j >= v)  f[j] = max(f[j], f[j - v] + w);
        }
    }
    cout << f[V] << endl;
    return 0;
}

买书

小明有 块钱，现有 10 元，20 元，50 元，100 元 的书

每本书可以购买多次，求小明有多少种买书方案？(要求花掉全部的钱)

利用完全背包即可

初始化：；啥都不买->仅有一种方案

复杂度

  1. 最朴素的枚举是
  2. 优化后
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1005;

int v[] = {0, 10, 20, 50, 100};
int f[N];
// f[j], 总体积恰好是j的方案的集合


int main()
{
    int n;
    cin >> n;
    f[0] = 1;  // 记得初始化初值
    for (int i = 1; i <= 4; i ++ )
    {
        for (int j = 0; j <= n; j ++ )
        {
            if(j >= v[i])  f[j] += f[j -v[i]];
        }
    }
    cout << f[n] << endl;
    return 0;
}

货币系统

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110, M = 25010;

int a[N], f[M];
// f[i]表示这个数能不能被其他数表示出来

int main()
{
    int T;
    cin >> T;
    while(T -- )
    {
        memset(f, 0, sizeof f);
        int n;
        cin >> n;
        for (int i = 1; i <= n; i ++ )
            cin >> a[i];
        sort(a + 1, a + 1 + n);  // 排序保证从小到大递推(类似埃氏筛的思想)
        f[0] = 1;  // 一定要记得初始化
        int ans = 0, m = a[n];
        for (int i = 1; i <= n; i ++ )
        {
            if(!f[a[i]]) ans ++ ;
            for (int j = a[i]; j <= m; j ++ )
            {
                f[j] |= f[j - a[i]];
            }
        }
        cout << ans << endl;
    }


    return 0;
}

多重背包

有个数限制的背包模型

有个数限制的背包模型

时间复杂度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 6010;

int f[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        int v, w, s;
        cin >> v >> w >> s;
        for (int j = m; j >= 0; j -- )
        { // 朴素的枚举选择多少个即可
            for (int k = 0; k <= s && k * v <= j; k ++ )
            {
                f[j] = max(f[j], f[j - k * v] + k * w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

二进制优化

问题 Ⅱ 是利用二进制进行优化

将一个大的整数拆成二级制下多个小的数，对这些数的集合进行一次 01 背包即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 2010;

int f[N];

int main()
{
    int n, V;
    cin >> n >> V;
    for (int i = 1; i <= n; i ++ )
    {
        int v, w, s;
        cin >> v >> w >> s;
        for (int k = 1; k <= s; k *= 2)
        {
            for (int j = V; j >= k * v; j -- )  // 01背包
            {
                f[j] = max(f[j], f[j - k * v] + k * w);
            }
            s -= k;
        }
        if(s) // 对剩余的再处理一次
        {
            for (int j = V; j >= s * v; j -- )
            {
                f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    cout << f[V] << endl;
    return 0;
}

单调队列优化

混合背包

混合背包 = 01 背包 + 完全背包 + 多重背包

全部转换成多重背包然后利用二进制优化即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;

int f[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ )
    {
        int v, w, s;
        cin >> v >> w >> s;
        if(s == 0)
            s = (m / v) + 1;
        if(s == -1)
            s = 1;
        for (int k = 1; k <= s; k *= 2)
        {
            for (int j = m; j >= k * v; j -- )
            {
                f[j] = max(f[j], f[j - k * v] + k * w);
            }
            s -= k;
        }
        if(s)
        {
            for (int j = m; j >= s * v; j -- )
            {
                f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

分组背包

将物品分为若干组，每个组内只能选择一个元素

  • 第一个循环枚举分组(不存可以优化掉空间)
  • 第二个循环枚举体积
  • 第三个循环枚举每个分组内选择哪一个元素

复杂度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110;

int f[N], v[N], w[N];

int main()
{
    int n, V;
    cin >> n >> V;
    for (int i = 1; i <= n; i ++ )
    {
        int s;
        cin >> s;
        for (int j = 1; j <= s; j ++ )
            cin >> v[j] >> w[j];

        for (int j = V; j >= 0; j -- )  // 枚举体积
            for (int k = 1; k <= s; k ++ )
                if(j >= v[k])
                    f[j] = max(f[j], f[j - v[k]] + w[k]);
    }

    cout << f[V] << endl;

    return 0;
}

金明的预算方案

分析：可以将每个主件及其附件看作一个物品组，记主件为 , 两个附件为 ,则最多一共有 4 种组合：

这四种组合是互斥的，最多只能从中选一种，因此可以将每种组合看作一个物品，那么问题就变成了分组背包问题

在枚举四种组合时可以使用二进制的思想，可以简化代码。

时间复杂度：分组背包的时间复杂度是 物品总数 总体积，因此总时间复杂度是 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <algorithm>
#include <cstring>
#define v first
#define w second

using namespace std;

const int N = 65, M = 32010;

typedef pair<int, int> PII;

PII master[N];
vector<PII> servant[N];
int f[M];

int main()
{
    int N, m;
    cin >> N >> m;
    for (int i = 1; i <= m; i ++ )
    {
        int v, p, q;
        cin >> v >> p >> q;
        p *= v;
        if(!q)  master[i] = {v, p};
        else  servant[q].push_back({v, p});
    }
    for (int i = 1; i <= m; i ++ )
    {
        for (int u = N; u >= 0; u -- )
        {
            for (int j = 0; j < 1 << servant[i].size(); j ++ )
            {
                int v = master[i].v, w = master[i].w;
                for (int k = 0; k < servant[i].size(); k ++ )
                {
                    //  利用二进制进行表达
                    //  二进制表达选择情况
                    if(j >> k & 1)
                    {
                        v += servant[i][k].v;
                        w += servant[i][k].w;
                    }
                }
                if(u >= v)  f[u] = max(f[u], f[u - v] + w);
            }
        }
    }
    cout << f[N] << endl;
    return 0;
}

背包问题求具体方案

基础的 01 背包，但是要求求出选取的是什么(字典序最小的方案)

状态表示： 表示从前 个物品中选，总容量为 的最优解

要使得字典序最小，则尽可能选择前面的元素

状态转移： ;

然后考虑得到具体方案(以第一个物品为例)

  • 说明选取了第 1 个物品可以得到最优解。

  • ，说明不选取第一个物品才能得到最优解。

  • ，说明选不选都可以得到最优解，

    但是为了考虑字典序最小，我们也需要选取该物品。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;

int f[N][N], v[N], w[N];


int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ )
    {
        cin >> v[i] >> w[i];
    }
    for (int i = n; i >= 1; i -- )
    {
        for (int j = 0; j <= m; j ++ )
        {
            f[i][j] = f[i + 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    }
    int j = m;
    for (int i = 1; i <= n; i ++ )
    {
        if(j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
        {
            cout << i << " ";
            j -= v[i];
        }
    }
    return 0;
}

机器分配

可以转化为分组背包， 同时要求出具体方案

倒推的时候通过 判断这个选不选

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 20;

int f[N][N], s[N][N], w[N][N], way[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            cin >> w[i][j];
    // 分组背包
    for (int i = 1; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ )
            for (int k = 0; k <= j; k ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);

    cout << f[n][m] << endl;

    int j = m;
    for (int i = n; i >= 0; i -- )
    {
        for (int k = 0; k <= j; k ++ )
        {
            if(f[i][j] == f[i - 1][j - k] + w[i][k])  // 求方案
            {
                way[i] = k;
                j -= k;
                break;
            }
        }
    }
    for (int i = 1; i <= n; i ++ )  cout << i << " " << way[i] << endl;
    return 0;
}

背包问题求方案数

大体思路一致，将维护最大值更改为维护总和

注意此时需要对 数组进行 初始化 ( )

先初始化所有的 为 1，因为背包里什么也不装也是一种方案

然后进行循环， 如果

  • 两种方案一样优，将增加
  • 新方案更优，更改 数组和 数组

复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int f[N], g[N];
// g数组维护方案数

int main()
{
    int n, V;
    cin >> n >> V;

    // 初始化
    for (int i = 0; i <= V; i ++ )
        g[i] = 1;

    for (int i = 1; i <= n; i ++ )
    {
        int v, w;
        cin >> v >> w;
        for (int j = V; j >= v; j -- )
        {
            if(f[j] == f[j - v] + w)
                g[j] = (g[j] + g[j - v]) % mod;
            else if(f[j] < f[j - v] + w)
            {
                f[j] = f[j - v] + w;
                g[j] = g[j - v];
            }
        }
    }

    cout << g[V] << endl;
}

有依赖的背包问题

在选择某个物品时有一个依赖关系，要求先选择该元素的前驱(类似没有上司的舞会)

-> 在树上的 01 背包

而以往的背包 DP 每个物品关系是任意的（但我们一般视为线性的）

所以，这题沿用背包 DP 的话，要从原来的线性 DP 改成树形 DP 即可

利用 vector 存图，每一次三重循环：

​ (子节点) -> (总空间) -> (子树的空间)

状态表示：表达选择以为子树的物品，在容量不超过时所获得的最大价值

复杂度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 110;

int f[N][N];
// f[x][v]表达选择以x为子树的物品，在容量不超过v时所获得的最大价值
int n, V;
int w[N], v[N];
vector<int> tr[N + 1];

void dfs(int x)
{
    for (int i = v[x]; i <= V; i ++ )  f[x][i] = w[x];
    // 选择点x
    for (auto t : tr[x])
    {
        dfs(t);
        for (int j = V; j >= v[x]; j -- )  // 枚举含有当前节点的总空间
        {
            for (int k = 0; k <= j - v[x]; k ++ )  // 枚举子树的空间
            {
                f[x][j] = max(f[x][j], f[x][j - k] + f[t][k]);
            }
        }
    }
}

int main()
{
    cin >> n >> V;
    int root = -1;
    for (int i = 1; i <= n; i ++ )
    {
        int p;
        cin >> v[i] >> w[i] >> p;
        if(~p) tr[p].push_back(i);
        else root = i;
    }
    dfs(root);
    cout << f[root][V] << endl;
    return 0;
}

贪心结合背包

能量石

利用类似于 国王游戏 和 耍杂技的牛 的思路(邻项交换法)

发现有可能存在最优解的某些宝石的贡献为 0，我们剔除了这些宝石。

假设最优解的能量石排列长度为 因为去掉了那些没有贡献的宝石，位置为：

那么对于任意两个位置

交换后两个宝石的贡献总和不会变得更大，即（假设之前的总时间为 ）：

整理后:

。 这样，我们只要以如上条件作为宝石间排序的条件，进行一次

因为对于其他形式的放置规律，必然可以通过交换满足的相邻的两项来得到更小值

那么最优解的坐标（新的坐标）一定满足：

那么，我们只要搞个 01 背包，作为费用， 作为价值 ( 为当前花费时长)

状态表示： 表示当前正好花 时间得到的最大能量

状态转移方程：

最后循环一次找到最大值即可

复杂度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 105, S = 10005;

int n;
int f[S];

struct Node{
    int s, e, l;
    bool operator < (const Node &x) const {
        return s * x.l < x.s * l;
    }
}a[N];

int main()
{
    int T;
    cin >> T;
    for (int cnt = 1; cnt <= T; cnt ++ )
    {
        memset(f, 0, sizeof f);
        int n;
        cin >> n;
        int t = 0; // 记录总和
        for (int i = 1; i <= n; i ++ )
        {
            int s,e, l;
            cin >> s >> e >> l;
            t += s;
            a[i] = {s, e, l};
        }
        sort(a + 1, a + 1 + n);
        for (int i = 1; i <= n; i ++ )
        {
            for (int j = t; j >= a[i].s; j -- )  // 01背包
            {
                f[j] = max(f[j], f[j - a[i].s] + max(0, a[i].e - (j - a[i].s) * a[i].l));
            }
        }
        int res = 0;
        for (int i = 1; i <= t; i ++ ) res = max(res, f[i]);
        printf("Case #%d: %d\n", cnt, res);
    }
    return 0;
}