树的最长路径

题意： 给定一个含有 个节点的树，以及树中每条边的权值

现需要在树中找出一条路径，使得该路径上所有边的权值之和最大

对于求树的直径问题，可以用两次 DFS 或者树形 DP 的方法在 时间求出树的直径

(两次 DFS 无法处理负权边)

两次 DFS/BFS

分析： 首先从任意节点 开始第一次 DFS，到达距离最远的节点，记为 , 然后再从 开始左第二次 DFS

到达距离 最远的节点， 记为 , 则 即为树的直径

证明：

显然，如果第一次 DFS 到达的节点 是直径的一端，那么第二次 DFS 到达的节点 一定是直径的一端。

我们只需证明在任意情况下， 必为直径的一端，即可证明上述分析的正确性

我们使用反证法，记出发节点为 y 设真实的直径是

则定理的反面为：进行的第一次 DFS 到达的节点 不为 或

共分三种情况：

  • 在直径 上

因为 距离 最远， 故

如果 此时 比直径更长，故矛盾

如果 此时说明 也是直径的一个端点

1
2
3
4
5
graph LR;
    s-->y;
    y-->c;
    c-->t;
    c-->z;
  • 不在直径 上， 和 存在重复路径

​ 因为 距离 最远， 故

​ 如果 此时 比直径更长，故矛盾

​ 如果 此时说明 也是直径的一个端点

1
2
3
4
5
6
graph LR;
    s-->c;
    y-->c;
    c-->c'
    c'-->t;
    c'-->z;
  • 不在直径 上， 和 不存在重复路径

​ 因为 距离 最远， 故

​ 此时 比直径更长，故矛盾

1
2
3
4
5
6
graph LR;
    s-->c;
    c-->t;
    c-->c'
    y-->c';
    c'-->z;

复杂度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 1e5 + 5;

int n, z;
int d[N];
vector<int> e[N];

void dfs(int u, int fa)
{
    for (auto v: e[u])
    {
        if(v == fa) continue;
        d[v] = d[u] + 1;
        if (d[v] > d[z]) z = v;
        dfs(v, u);
    }
}

int main()
{
    cin >> n;
    for (int i = 1; i < n; i ++ )
    {
        int a, b;
        cin >> a >> b;
        e[a].push_back(b);
        e[b].push_back(a);
    }
    dfs(1, -1);  //  随意取一个点为最初点
    // dfs完后 z已经被更新为距离起始点最远的点了
    d[z] = 0; // 恢复一下
    dfs(z, 0); // 第二次dfs
    cout << d[z] << endl;
    return 0;
}

树形 DP

分析： 我们记录当为树的根时，每个节点作为子树的根向下，所能延伸的最远距离 ，和次远距离 ，那么直

径就是所有 的最大值

状态表示： , 分别表示从 往下的最长路径和次长路径( 和 分别对应 的不同子节点)

状态计算： 取全局最大值

复杂度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5 + 5;

typedef pair<int, int> PII;
int n, ans = -2e9;
int d1[N], d2[N];
vector<PII> e[N];

void dfs(int u, int fa)
{
    d1[u] = d2[u] = 0;
    for (auto x: e[u])
    {
        int v = x.first, w = x.second;
        if(v == fa)  // 保证只往下搜索
            continue;
        dfs(v, u);
        int t = d1[v] + w;
        if (t > d1[u])  // 更新最远距离(新次远距离等于旧最远距离)
            d2[u] = d1[u], d1[u] = t;
        else if(t > d2[u])  // 更新次远距离
            d2[u] = t;
    }
    ans = max(ans, d1[u] + d2[u]);
}

int main()
{
    cin >> n;
    for (int i = 1; i < n; i ++ )
    {
        int a, b, w;
        cin >> a >> b >> w;
        e[a].push_back({b, w});
        e[b].push_back({a, w});
    }
    dfs(1, -1);  // 任意选取一个节点作为根节点
    cout << ans << endl;
    return 0;
}

树的中心

题意： 给定一棵树，树中包含 个 节点 和 条 无向边，每条边都有一个权值

请在树中找到一个点，使得该点到树中其他结点的最远距离最近, 输出这个最远距离

分析：

这个问题是树形 DP 中的一类经典模型，常被称作换根 DP， 一般分为三个步骤：

  • 指定任意一个根节点

  • 一次 dfs 遍历，统计出当前子树内的节点对当前节点的贡献(距离)

  • 一次 dfs 遍历，统计出当前节点的父节点对当前节点的贡献(距离)，然后合并统计答案

对于一个节点，我们先 dfs 预处理了每个点以该节点为根，走的的最远距离和次远距离后

如果想要求出树中离该节点最远的距离时，可以分为以下两种子情况 (以 为例)

  • 最远距离出现在该节点往下走的路径中 ( 和 中显然取 更好)

  • 最远距离出现在该节点往上走的路径中，此时需要额外考虑 的父节点 取 时选取的子节点是否是

    可以想到，如果我们在第一次 dfs 将节点 取到最远距离时的子节点记为 , 那又可以分为以下两种情况

    • 那么可以用 ( 往下的最远距离) 进行转移
    • 那么就只能用 ( 往下的次远距离) 进行转移, 因为不可以从 往上到 又往下走回 
1
2
3
4
5
6
graph TD;
	u --> v;
	u --> d1_u;
	u --> d2_u;
	v --> d1_v;
	v --> d2_v;

故在整个过程之中，对于一个节点 需要记录的有

  • 往下走的最远距离 (往子节点 走)
  • 往下走的次远距离
  • 每个点往上走的最远距离

那么，最后遍历所有节点，取 中最小的即可

状态表示：

  • 往下能走到最远距离
  • 往下能走到的次远距离
  • 存下 节点向下走的最长路径是从哪一个节点下去的
  • 往上走的最远距离

状态计算：

用最远距离更新

用次远距离更新

取全局最大值

复杂度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10010, INF = 0x3f3f3f3f;

typedef pair<int, int> PII;

int n;
vector<PII> e[N];
int d1[N], d2[N], s1[N], up[N];

void dfs1(int u, int fa)
{
    d1[u] = d2[u] = -INF;  //本题边权都是正的，可以不用初始化为负无穷
    for (auto [v, w]: e[u])
    {
        if(v == fa) continue;
        dfs1(v, u);
        int t = d1[v] + w;
        if (t > d1[u])
        {
            d2[u] = d1[u];
            d1[u] = t;
            s1[u] = v;
        }
        else if(t > d2[u])
        {
            d2[u] = t;
        }
    }
    // 如果初始化为负无穷需要特判叶子节点
    if(d1[u] == -INF) d1[u] = d2[u] = 0;
}

void dfs2(int u, int fa)
{
    for (auto [v, w]: e[u])
    {
        if (v == fa) continue;
        if (s1[u] == v)  up[v] = w + max(up[u], d2[u]);  // son_u = v, 用次远距离更新
        else up[v] = w + max(up[u], d1[u]);  // son_u != v, 用最远距离更新
        dfs2(v, u);
    }
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        e[a].push_back({b, c});
        e[b].push_back({a, c});
    }

    dfs1(1, -1);  // 处理向下的最远距离和次远距离
    dfs2(1, -1);  // 处理向上的最远距离

    int ans = INF;
    for (int i = 1; i <= n; i ++ ) ans = min(ans, max(d1[i], up[i]));

    cout << ans << endl;

    return 0;
}

数字转换

题意： 如果一个数 的 约数之和 y(不包括他本身)比他本身小，那么 和 可以互相转换

给定一个正整数 ，求出在由正整数 构成的数集中：在不出现重复数字的情况下，能进行的最大变换步数

分析： 首先我们考虑如何处理约数之和，如果对于每一个 之间的数，我们采用朴素的试除法进行处理，

复杂度为 是可能会超时的，所以换一种 的方法我们可以考虑对于当前枚举到的数 ，枚举

对 之间的数的贡献，显然 能使得 的约数之和都增加 ( 不是 的约数)

然后处理转换的问题，如果 的约数之和 比它本身小, 那么 和 可以互相转换，等价于可以在 x 和 y

之间连一条无向边，由于每个数的约数之和是确定的，所以所有的这样的边一起组成了一个森林 🌴

这样要求的最大转换步数就可以转化求解为这个森林中的树的直径的最大值，

类比上面的树的最长路径，可以枚举每个点作为根的情况，然后取全局最大值即可

但是搜索时爆栈了 ❓

这说明存储的这个过程还有优化的空间，其实由于我们枚举了每一个点作为根节点的情况，所以每次只需要存入一

条有向边即可， 同时要采用记忆化的搜索方式

状态表示： , 分别表示从 往下的最长路径和次长路径( 和 分别对应 的不同子节点)

状态计算： 取全局最大值

复杂度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 50005;

int a[N], d1[N], d2[N];
int ans = -2e9;
vector<int> e[N];

void dfs(int u)
{
    if (d1[u])  // 记忆化
        return;
    for (auto v: e[u])
    {
        dfs(v);
        int t = d1[v] + 1;
        if (t > d1[u])
        {
            d2[u] = d1[u];
            d1[u] = t;
        }
        else if (t > d2[u])
            d2[u] = t;
    }
    ans = max(ans, d1[u] + d2[u]);
}

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ )
        for (int j = 2; j <= n / i; j ++ )  // 从2开始, 一个数的约数不含它本身
            a[i * j] += i;

    for (int i = 1; i <= n; i ++ )
        if(i > a[i])
            e[a[i]].push_back(i);  // 虽然是可以双向转移，但是实际上只需要连一条有向边即可(因为会枚举所有的情况)

    for (int i = 1; i <= n; i ++ )
        dfs(i);   // 枚举以每一条边为根节点的情况

    cout << ans << endl;

    return 0;
}

二叉苹果树

题意： 给定一棵含有 个结点的树，树根编号为 1，且树上的每条边有一个边权

要求我们进行减枝，只保留树中的 条边，使得树根(编号为 1)所在的连通块的所有边的边权之和最大

分析： 这题的本质其实是有依赖的背包模型，不同点在于把物品价值分配给了边而不是点

不过对于树结构来说，每一个节点的入边仅有一条，所以可以将每一个节点的入边权视作该点的价值

对于有依赖的背包问题，有两种常见的处理方式

  • 按子物体体积集合划分
  • 分组背包集合划分, 将依赖关系转化为多种组合

这里采用体积(边数)划分方案复杂度较低, 枚举当前节点的边数和子树内的边数进行转移即可

状态表示： 表示以 为根节点的子树，联通块内边数不超过 的情况下边权最大值

状态计算： (枚举以 为根的子树内边数 )

复杂度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;

const int N = 105;

int n, m;
int f[N][N];
vector<PII> e[N];

void dfs(int u, int fa)
{
    for (auto [v, w]: e[u])
    {
        if (v == fa) continue;
        dfs(v, u);
        for (int j = m; j >= 0; j -- )  // 枚举边数
            for (int k = 0; k <= j - 1; k ++ )  // 枚举子树的边数(留一条用于从 u --> v )
                f[u][j] = max(f[u][j], f[u][j - k - 1] + f[v][k] + w);
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i < n; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        e[a].push_back({b, c});  // 无向边
        e[b].push_back({a, c});
    }
    dfs(1, -1);
    cout << f[1][m] << endl;
    return 0;
}

没有上司的舞会

题意： 给定一棵含有 个结点的树，树根编号为 1，且树上的每条节点有一个权值 ，对于每一条边，仅能

选取一个端点，求选取节点使得权值之和最大

分析： 对于一个节点是否选取会对其他决策产生影响，所以我们需要在状态转移的时候记录下当前节点的状态

也就是状态机模型，可以单独开一维用于记录是否选取该节点，然后考虑对于当前节点，有两种转移方式

  • 对于不选当前节点的，子节点可选可不选
  • 对于选取了当前节点的，由于一条边上只能选取一个点，所以子节点一定不能选择

最后取 和 中的较大值即位答案

状态表示：

  • 以 为根的子树中选择，并且不选 这个点的权值之和最大值

  • 以 为根的子树中选择，并且选择 这个点的权值之和最大值

状态计算： 对于当前节点 的所有子节点

  • 没选取 ，可以选择
  • 选取了 ，不能选取

复杂度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 1e4 + 5;

int n;
int a[N], fa[N];
int f[N][2];
vector<int> e[N];

void dfs(int u)
{
    f[u][1] = a[u];  // 加上当前节点的值
    for (auto v: e[u])
    {
        dfs(v);
        f[u][0] += max(f[v][0], f[v][1]);
        f[u][1] += f[v][0];
    }
}

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ )
        cin >> a[i];

    for (int i = 1; i < n; i ++ )
    {
        int a, b;
        cin >> a >> b;  // b 是上司
        e[b].push_back(a);
        fa[a] = 1;  // 有上司，用于判断根节点
    }
    for (int u = 1; u <= n; u ++ )
    {
        if (!fa[u])  // 找到根节点
        {
            dfs(u);
            cout << max(f[u][0], f[u][1]) << endl;
            break;
        }
    }
    return 0;
}

战略游戏

题意： 给定一棵包含 个结点的 树，以及树上的 条边

我们需要在这 个结点中，选择一定数量的结点放上哨兵

最终要求，对于树中的每一条边边的左右两端，至少有一个结点上放置了哨兵

求解一个方案，使得放置的哨兵数量最少，输出该方案放置的哨兵数量

分析： 本题与上一题没有上司的舞会十分类似，考虑以结点 为 根节点 的子树，该子树所有的方案

可以由当前结点放或不放哨兵进行划分

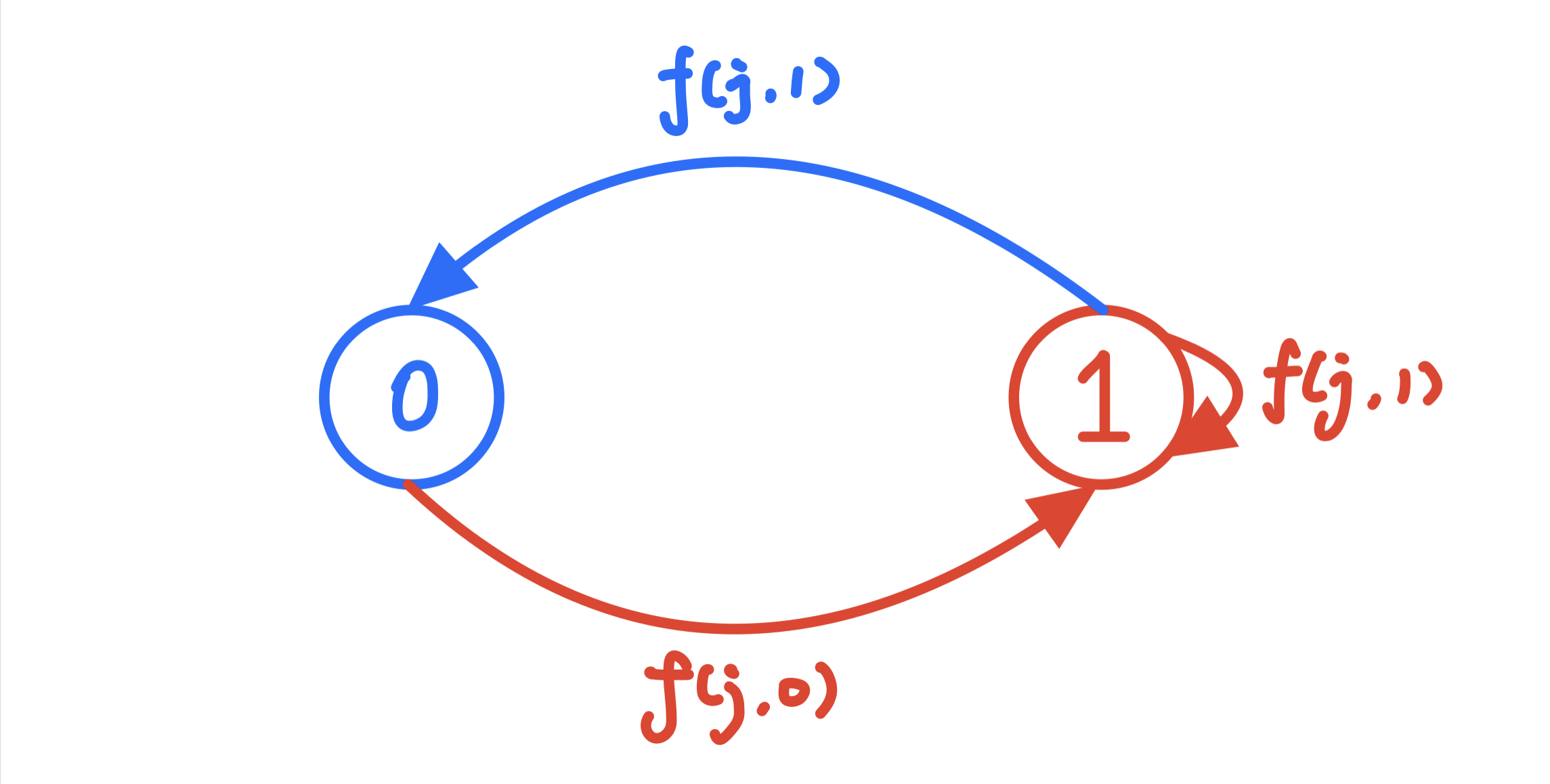
这也是一种 状态机模型(借图)

pic
  • 如果当前结点没有放哨兵(0)，则该子树中，连边的另一端，必须放置哨兵(1)
  • 如果当前结点放置了哨兵(1)，则该子树中，连边的另一端，可以放置哨兵(1)，也可以不放置哨兵(0)

状态表示：

  • 以 为根的子树中， 这个点的不放置哨兵的最少哨兵总数

  • 以 为根的子树中， 这个点的放置哨兵的最少哨兵总数

状态计算： 对于当前节点 的所有子节点

  • 没选取 ，必须选择
  • 选取了 ，可选择 也可以不选择

复杂度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 1505;

int n;
int fa[N];
int f[N][2];
vector<int> e[N];

int dfs(int u)
{
    f[u][0] = 0, f[u][1] = 1;  // 初始化
    for (auto v: e[u])
    {
        dfs(v);
        f[u][0] += f[v][1];
        f[u][1] += min(f[v][0], f[v][1]);
    }
}

int main()
{
    while(cin >> n)
    {
        memset(fa, 0, sizeof fa);
        memset(e, 0, sizeof e);
        for (int i = 1; i <= n; i ++ )
        {
            int a, b, siz;
            scanf("%d:(%d)", &a, &siz);
            while (siz -- )
            {
                cin >> b;
                e[a].push_back(b);
                fa[b] = true;  // 用于判断根节点
            }
        }
        for (int u = 0; u < n; u ++ )
        {
            if (!fa[u])
            {
                dfs(u);
                cout << min(f[u][0], f[u][1]) << endl;
            }
        }
    }

    return 0;
}

皇宫看守

题意：给定一个含有 个结点的树

每个结点有一个 权值 表示在第 个点上放置哨兵的花费

对于每个哨兵来说，他可以观察当前结点，以及所有与当前点相连的相邻结点

求解一种放置哨兵的方案，使得每个结点都被观察到，且方案的花费最小

分析： 本题还是状态机模型，所以对于每一个节点，有三种情况

  • 父节点放置哨兵，所有子节点都可放可不放哨兵
  • 父节点不放哨兵，但是他至少有一个子节点放置哨兵，观察住了他
  • 父节点不放哨兵，但父节点的父节点放置哨兵观察，则子节点可放可不放哨兵

可以简化为三个点的状态机模型

  • 被父节点观察 (0)
  • 被子节点观察 (1)
  • 被自己观察 (2)

状态表示：

  • 以 为根的子树中， 这个点的父节点放置哨兵的最少花费
  • 以 为根的子树中， 这个点的至少其中一个子节点放置哨兵的最少花费
  • 以 为根的子树中， 这个点的至少其中一个子节点放置哨兵的最少花费

状态计算： 对于当前节点 的所有子节点

  • 没选取 ， 可选可不选

  • 枚举子节点，当选取了其中的一个子节点 ，则其余所有子节点()可选可不选

    而 其中

  • 选取了 ，则子节点 随意， 注意要加上 的权值

复杂度： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1510;

typedef pair<int, int> PII;

int n;
vector<int> e[N];
bool fa[N];
int w[N], f[N][3];

void dfs(int u)
{
    f[u][0] = 0;    // 被父节点观察
    f[u][1] = 2e9;  // 被某个子节点观察, 先初始化为最大值
    f[u][2] = w[u]; // 被自己观察
    for (auto v: e[u])
    {
        dfs(v);
        f[u][0] += min(f[v][1], f[v][2]);
        f[u][2] += min(min(f[v][0], f[v][1]), f[v][2]);
    }
    for (auto v: e[u])
    {
        //f[u][0]中记录了sum{min(f(u_son,1), f(u_son,2))}，再从中减去v的贡献即可
        f[u][1] = min(f[u][1], f[v][2] + f[u][0]  - min(f[v][1], f[v][2]));
    }
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ )
    {
        int a, cost, cnt;
        cin >> a >> cost >> cnt;
        w[a] = cost;
        for (int i = 1; i <= cnt; i ++ )
        {
            int b;
            cin >> b;
            e[a].push_back(b);
            fa[b] = 1;  // 判断是否是根节点
        }
    }
    for (int u = 1; u <= n; u ++ )
    {
        if (!fa[u])  // 是根节点
        {
            dfs(u);
            cout << min(f[u][1], f[u][2]) << endl;
        }
    }
    return 0;
}